汽轮机调节阀的升程流量特性无例外的是非线性的,而信号与调节阀的升程关系是线性的,这样必然导致机组调节系统的静态特性是非线性的。非线性静态特性不能保证机组良好的调节特性,在某些情况下将导致系统不能正常工作。因此,在汽轮机调节系统设计时,往往通过非线性补偿的方式将调节阀特性线性化。然而,非线性补偿后,对系统的响应特性有哪些影响,其影响的程度如何,到目前为止还没有进行研究,有些机组由于补偿特性不合理,导致系统摆动,机组的正常运行受到很大的影响。另外,电力系统正在进行机组一次调频特性的实验研究和调节系统的参数测试,这种非线性补偿对于一次调频特性和参数测试结果的影响也需要进行系统的分析。因此有必要对非线性补偿特性进行研究,提供机组设计和调整的依据,特别是对DEH控制系统的补偿特性提供调整的参考,同时,为机组参数测试提供正确的模型,具有重要的工程实用价值。
1 非线性补偿的形式
常规液压调节系统中,阀门特性的线性化通过两个途径来实现:调节阀开启的重叠度和配汽凸轮型线的调整。通过改变阀门的重叠度实现特性的线性化,必然导致节流损失的增加,在采用提板配汽的中小机组中比较常见,当采用凸轮配汽时,凸轮的转角与油动机升程满足线性关系,而阀门升程则取决于凸轮转角与凸轮升程的关系,通过改变凸轮转角与升程的关系就可以在同样转角条件下增加或者减小阀门开度的变化量,从而实现阀门特性的线性化,在凸轮型线应保证不会发生自锁,并尽量减小凸轮的受力以减小磨损。采用凸轮配汽方式实现静态特性线性化时,调节系统的数学模型如图1所示。
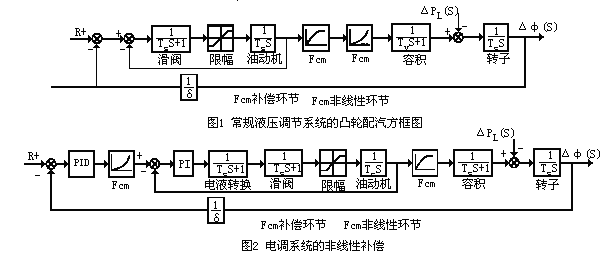
目前,电调系统,也就是常说的DEH控制系统得到普及,在电调系统中,为了使得阀门特性线性化,通过所谓的电子凸轮来实现调节阀特性非线性的线性化,其实质是通过控制信号的非线性补偿使得流量特性线性化。使用最为广泛的是在计算机内部进行信号的补偿,其数学模型如图2所示,将输出到电液转换器之前的信号进行补偿。相对于同样信号变化,当流量变化小时,将信号放大,增加阀门开度的变化量,也就是增加阀门流量的变化量,当流量变化大时,将信号缩小,使得对应于同样的信号变化,具有相同的流量变化量,以达到机组静态特性的线性化。
在图1和图2中,R为转速给定;ΔPL(s)为负荷扰动;Δφ(s)为转速变化;Td为电液转换器时间常数;Tk为滑阀时间常数;Ts为油动机时间常数;Tv为容积时间常数;Ts为转子时间常数;δ为调速不等率。
2 常规液压系统
对于图1所示的常规液压系统,通过凸轮型线的变化来实现阀门特性非线性的补偿,此时抽动机的行程没有变化,发生变化的只是阀门的升程,从理论上来说,非线性补偿不会影响机组的动态响应特性。当油动机滑阀的输出发生限幅时,情况也是相同的。
图3为10%负荷扰动后的动态响应曲线。按照单机运行方式进行仿真,没有考虑电网对于系统稳定的影响。机组并列运行时,考虑到电网的作用,系统的稳定性将得到改善。
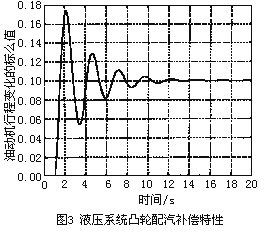
由于非线性补偿在油动机之后,小扰动条件下,油动机滑阀不会出现限幅,因此,系统实际上是一个线性系统。在阀门特性变化比较陡的地方,升程流量的变化率小于1,为1/K值,则阀门特性非线性补偿环节,即油动机升程与阀门升程之间的变化率必然大于1,为K值,这样油动机升程与流量之间的关系即为线性关系,也就是说信号变化与流量变化之间为线性关系。由于两个环节串联,一个环节为K,随后一个环节为1/K,环节简化的结果是等效于一个放大系数为1的环节,也就是说系统线性化了。大量的仿真结果表明,在常规的液压调节系统中,通过配汽凸轮型线的非线性补偿,不会引起系统动态特性的恶化,系统的动态响应特性和一次调频特性完全取决于调节系统,与补偿环节没有关系。
3 数字电液调节系统
3.1 油动机滑阀不限幅时的特性
对于数字电液调节系统(DEH系统)来说,非线性补偿在电液转换器之前,通过非线性函数来实现,如图2所示,非线性补偿环节的输出信号与油动机的阀位反馈信号进行比较之后,其误差信号经过PI控制器,驱动电液转换器,使油动机滑阀运动,控制油动机。对于不同的阀门开度,同样的阀门升程对应的流量变化是不同的,在阀门刚开启的时候,同样升程对应的流量变化近似为线性,因为此时阀门处于临界流动状态,但随着阀门开度的增加,阀后压力增加,阀门的流动转向非临界,流量变化量减小,若在考察的点上,阀门升程流量关系曲线的斜率为1/K(K>1),为了保证流量特性线性,对于同样的信号变化,则必须增加阀门开度,相当于增加油动机行程的变化量,因此,非线性补偿环节输入与输出信号之间的斜率必须等于K值,这样就可以保证在静态条件下,信号变化量与流量变化量之间满足线性规律。补偿环节的放大系数K分别为0.1、1、10、100时的仿真试验结果表明,当油动机滑阀没有限幅时,扰动作用后,补偿环节的存在对系统的响应特性没有任何影响,对应于不同的K值,系统的过渡过程特性相同。
这是因为油动机滑阀没有限幅,在进行系统传递函数简化时,非线性补偿环节与阀门特性非线性环节互为倒数,相互抵消,滑阀和油动机的运动没有限制,在阀门升程流量特性斜率小于1时,同样信号变化要求更大的油动机位移,由于滑阀的运动没有受到输出阀值的限制,补偿环节增加了油动机滑阀的输入信号,使油动机的动作速度加快,以保证达到更大的位移所需要的时间不随工况点的变化而变化,因此,非线性补偿不会影响系统的稳定性和一次调频特性,系统的动态性能取决于除补偿环节以外的各个组成环节的特性。
3.2 油动机滑阀限幅时的特性
然而,油动机滑阀的行程是有限的,取决于其控制油口的高度。当滑阀的行程超过此高度后,输出不再变化,也就是说滑阀输出到油动机的有用信号受到了限幅。当限幅值为±1.0,负荷扰动值为10%,补偿环节放大系数K值变化时的动带响应特性如图4所示。
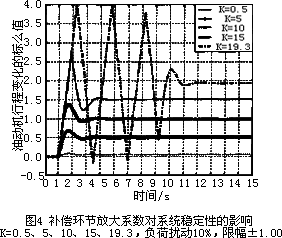
从图4的动态相应特性可见,随着补偿环节放大系数(对应斜率)的增加,系统的稳定性逐渐降低,达到稳态和最大值的时间延长,相当于系统的反应速度降低,当限幅值为±1.0时,10%负荷扰动可以维持系统稳定的最大补偿放大倍数为19.3,当放大系数大于19.3时,系统不稳定,当放大倍数为6.7时,滑阀开始限幅。在滑阀的运动发生限幅之后,油动机的运动速度和达到最大值与稳态值的时间发生变化。因此,为了保持系统的稳定,当油动机滑阀的限幅值为±1.0,补偿环节的放大倍数不能够大于19.3。
由此可见,油动机滑阀运动的限幅,随着补偿环节放大倍数的变化,将影响系统的稳定性。通过仿真试验对油动机滑阀不同限幅时的特性进行了研究,滑阀限幅分别为:±1.05、±1.10、±1.15和±1.30时,补偿环节的放大系数K分别在:7.05、7.41、7.76和8.86时抽动机滑阀开始限幅,对系统的动态响应特性发生影响,当K值分别达到:20.28、21.25、22.22和25.11时系统处于临界稳定,K值继续增加时系统不稳定。不同限幅和补偿环节放大倍数时的动态响应特性曲线与图4相似。
随着限幅值的增加,补偿环节的最大放大倍数增加,对应于每一个限幅值,有一个极限放大倍数,当补偿环节的放大倍数大于该极限值之后,系统不稳定。当滑阀限幅开始起作用后,油动机的运动速度受到限制,系统达到稳态的时间延长。不同限幅值所对应的极限放大倍数和油动机滑阀开始限幅的放大倍数如表1所示。
表1 滑阀限幅值与补偿环节放大倍数的关系(10%扰动)
| 限幅值 |
限幅开始K值 |
临界K值 |
| ±1.0 |
6.7 |
19.3 |
| ±1.05 |
7.05 |
20.28 |
| ±1.10 |
7.41 |
21.25 |
| ±1.15 |
7.76 |
22.22 |
| ±1.30 |
8.86 |
25.11 |
实际上,对于确定的系统,其滑阀限幅值和非线性补偿环节的最大放大系数K值是确定的,因此,要保证系统稳定,对于不同的限幅值和放大倍数K,就有不同的允许最大扰动负荷。仿真试验确定的不同限幅和放大系数时的最大扰动负荷如表2所示。当扰动负荷小于对应的数值时,系统是稳定的,当扰动负荷大于对应的数值时,系统是不稳定的。这样,对于确定的系统,其限幅值和补偿环节放大倍数是已知的,可以通过限制负荷扰动的大小来保证系统的稳定性。
了解更多产品详情请登录http://www.zjcz-v.com

